The well in Egypt

The fact that the Earth is a globe is by no means a new thing: the circumference of the Earth was calculated already in 200 B.C., and therefore the newly famed notion of flat Earth would mean ignoring common knowledge that people had already over 2,000 years ago.

All that was required for this observation in those ancient times was a realization that we must be dealing with some curvature in the first place, followed by the use of a stick, some additional legwork for distance estimation and some basic arithmetics. Anyone could repeat this experiment today, and it has actually been done several times in various science shows on television.

The context for this is easiest to do if one of the places used for measuring happens to have the Sun shining down from the zenith, but it gets only a little more complicated if done at other locations.

Every year, on a day called the Summer Solstice, the Sun appears to be directly overhead the Tropic of Cancer, which means that any straight-standing objects do not leave visible shadows, and if you have a hole dug into the ground, the Sun's rays will reach the bottom of such a hole at noon. Most such holes in ancient times were open wells, so this phenomenon is very noticeable, as the sunlight gets reflected back from the surface of the water at the bottom of the well.

A Greek astronomer, geographer and mathematician called Eratosthenes had noted that in the Egyptian city that is today known as Aswan, this rare event happened during the Summer Solstice, and hence the Sun had to be directly overhead the city on that day. But Eratosthenes was also aware that the same phenomenon never happens in Alexandria some 800 km further north: even on the day of the Summer Solstice, tall towers still cast a short shadow.

Based on this easily verifiable fact Eratosthenes concluded that such a difference can only be explained if the surface of the Earth is curved, so he recorded the angle of the shadow in Alexandria and by knowing the approximate distance between Aswan and Alexandria, he came out with a number for the circumference that was just a few percentages off from the value that we know today.

This was a remarkable feat, considering the many uncertainties that he had at the time:

Alexandria was not exactly due north from Aswan, so this caused a slight distortion to the measured curve;

Figuring out the distance between these two cities by using the means available at the time was inaccurate;

And finally, Aswan is not exactly on the Tropic of Cancer, but some tens of kilometers north of it, yet for any shallow wells that must have been the norm, thanks to the river Nile that flows past Aswan, that tiny error did not make big enough difference to be notable.

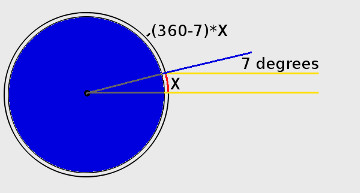
Therefore, by calculating that the angle of the shadow in Alexandria was roughly 7 degrees and using the distance estimation between the cities, he came out with a figure that was totally acceptable, considering all the imprecision that was unavoidable at the time: it was within 10-15% of the actual value.

The attached figure shows the idea: if the angle between the cities was 7 degrees, the distance between the cities would therefore be 7/360 of the circumference of the Earth. Therefore, the whole circumference would be 51.4 times the distance between the cities.

Despite the fact that the results of Eratosthenes' work had been written down, it still took some 1,700 years until the same conclusion was fully accepted in Europe, but when Columbus set on his voyage that eventually led him to America, he was already well aware of the fact that the Earth is a globe: after all, Columbus was trying to find a new route to India by going west instead of east, clearly understanding that the Earth was a globe. In fact, the very oldest surviving globe model of the Earth, the Erdapfel, was created by Martin Behaim in 1492, just prior to Columbus' return: it clearly depicts the Earth as a sphere, but does not contain the American continent yet, for obvious reasons.

First recorded note of a globe of the Earth refers to the version made by another Greek philosopher, Crates, and this reference dates back to some 100 years after Eratosthenes' observations. So the Greek quickly accepted the results of his work.

Hence, if we accept the assumption that the Earth is flat, then we also have to accept that the conspiracy over the globe Earth started really, really early, and it is therefore not just the most successful conspiracy ever, but also most likely the oldest one. This is a remarkable feat, especially when it is over an issue that seemingly has no real value whatsoever for the average Joe.

Eratosthenes did not stop here: he also managed to estimate the tilt of the Earth's axis within one degree from the 23.4 degrees that we know it is today. All this over 2,000 years ago.

Unfortunately, some 100 years later, the advances in cartography were done by another Greek mathematician, Ptolemy, who had done his own approximation of the circumference of the Earth, but had grossly underestimated it.  But thanks to his great work in making maps, this wrong approximation remained an assumed fact for about 1,500 years, to the great disappointment of Ferdinand Magellan, as will be discussed in the next extra chapter.

As mentioned in the book, if you take the results of Erastosthenes' measurements and apply then wrongly to mean the parallax of a flat-Earth Sun, you get the infamous 5,000 km estimate for the altitude of the Sun.

But if you expect parallax to be the cause for these measurements, it should affect everything else with the Sun as well: the fact that the Sun rises from due east and sets in due west at equinox would not simply be possible, yet it happens twice every year, everywhere.

This, combined to the missing size changes throughout the day, is yet another nail in the coffin of flat Earth.

You can use just sticks, shadows and simple arithmetic to calculate the circumference of the Earth, as was done already over 2,000 years ago.